یک مسئله از آنالیز(اثبات از:سعید علیخانی)

آیا مجموعه z کامل است؟

مسئله ای از لایب نیتس

 

پاداش مخترع شطرنج

روایت کرده اند که حکمران هند که به سختی تحت تاثیر اختراع بازی شطرنج قرار گرفته بود ، به مخترع آن وعده داد که هر پاداشی بخواهد به او بدهد. مخترع تقاضایی کرد که به ظاهر خیلی ناچیز به نظر می رسید: او مقداری دانه های گندم در خواست کرد ، به نحوی که اگر آنها را در خانه های صفحه شطرنج جا دهند ، در هر خانه دو برابر خانه قبل وجود داشته باشد.به این ترتیب تعداد دانه های گندمی که او تقاضا کرد مساوی مجموع جمله های یک تصاعد هندسی بود که جمله اول آن ۱، قدر نسبتش ۲، و تعداد جمله هایش مساوی ۶۴ بود.

حکمران هند که ثروتمند ترین مرد جهان بود ، نتوانست از عهده این در خواست برآید.در حقیقت این راجه ثروتمند شرقی با همه تصورات بی پایان خود نتوانست این مقدار گندم را تهیه کند!!!!!

تعداد دانه های گندم برابر است با مجموع توانهای متوالی ۲ از ۰ تا ۶۳ یعنی:

۱۸ُ۴۴۶ُ۷۴۴ُ۰۷۳ُ۷۰۹ُ۵۵۱ُ۶۱۵ عدد گندم

اگر در هر سانتیمتر مکعب ۲۰ دانه گندم قرار بگیرد رویهم این تعداد گندم به اندازه ۹۲۲ُ۳۳۷ُ۲۰۳ُ۶۸۵ متر مکعب گندم می شود(۲۰ میلیون گندم در هر متر مکعب)

برای اینکه بتوان این مقدار گندم را بدست آورد باید هشت بار تمام زمین را کاشت و هشت بار محصول آنرا جمع کرد. به عبارت دیگر این محصول را از سیاره ای می توان بدست آورد که سطح آن هشت برابر زمین باشد.

به این ترتیب مخترع شطرنج درس خوبی به حکمران هند داد و به او ثابت کرد که امکانات بی ژایانی ندارد و نمی تواند "هر" خواهش مخترع را برآورد.

معادله درجه 4 از دکارت

    

مسابقات و جوايز مهم در دنیای رياضيات

  Abel : از جمله جوایز جدید در دنیای ریاضیات است که از طرف آکادمی علوم نروژ به مناسبت بزرگداشت تولد نیلز هنریک آبی (Niels Nenrik Abel 1802-1829) از سال 2003 به مناسبت دویست امین سالگرد تولد این ریاضی دان به محققین ریاضی اعطا می شود.

Cole : برای پاسداشت خدمات پروفسور فرانک نلسون کول (Frank Nelson Cole) از موسسین انجمن ریاضیات آمریکا، این انجمن دو جایزه در زمینه های جبر و تئوری اعداد به ریاضی دانان و محقیقن علم ریاضی اعطا می شود.

Eternity : نوعی پازل است که توسط کریستوفر مانکتون (Christopher Monckton) اختراع شد و شامل 209 تکه م یباشد که هر کدام یک چند ضلعی هستند که زوایای داخلی آنها 30 یا 60 یا 90 درجه می باشد. این پازل در سال 1999 در انگلستان معرفی شد و هدف آن ساختن پازل به گونه ای است که تشکیل یک دوازده وجهی - از نوع dodecagon - را بدهد. این جایزه مبلغ یک میلیون پوند بود که در سال 2000 به دو ریاضی دان که مسئله را حل کردند اعطا شد. چند سال بعد یک ریاضی دان دیگر چیدمان دیگری از این پازل را حل کرد و جایزه دیگری را نصیب خود کرد.

Fields Medal : این جایزه بسیار شبیه به جایزه نوبل در ریاضیات است. همانطور که ممکن است بدانید جایزه صلح نوبل به ریاضیای دانان اعطا نمی شود. اما Field Medal هر چهار سال یکبار از طرف اتحادیه بین المللی ریاضیات به محققان ریاضی اعطا می شود. این جایزه برای اولین بار در سال 1924 از طرف یک کنگره بین المللی در تورنتو (Toronto) تعیین شد. این جایزه بالاترین جایزه و پاداش در زمینه ریاضیات است که ممکن است به شخصی تعلق بگیرد. این جایزه یک مدال طلا است که ارزشی معادل پانزده هزار دلار دارد.

IMO : در عالم ریاضی جوایز بسیاری در مسابقات بین الملی به برترین ها اعطا می شود که شاید بزرگترین و معتبرترین آنها مسابقات بین المللی المپیاد ریاضی (The International Mathematical Olympiad) است. IMO مجموعه مسابقات همه ساله برای دانش آموزان دبیرستانی در کشورهای مختلف انجام می شود. اولین IMO در سال 1959 در رمانی برگزار شد و به تدریج گسترش پیدا کرد بگونه ای که امروزه بیش از 80 کشور در آن شرکت می کنند.

Putnam : از دیگر مسابقات مهم می توان به مسابقات Putnam که در آمریکای شمالی برگزار می شود اشاره کرد. این مسابقات برای داشنجویان راضی برقرار می شود و همه ساله در اول دسامبر بیش از 2000 دانشجو در دو جلسه و در مجموع شش ساعت به حل 12 مسئله ریاضی می پردازند. اغلب مسائل سخت هستند و راه حل های عادی ندارند.

MCM : یا International Mathematical Contest in Modeling نوعی از مسابقات تیمی دانشجویی است. مسائل این مسابقات اغلب توسط مسئولین دولتی یا دست اندرکاران صنعتی طراحی می شود. بهترین راه حل ها در ژورنالها و مجله های معتبر منتشر می شوند.

Nevanlinna : جایزه ای است که از طرف اتحادیه بین الملی ریاضیات به محققین در زمینه علوم اطلاعات (Information Science) اعطا می شود. افراد برنده همانند Field Medal جایزه دریافت می کنند، این جایزه برای اولین بار در سال 1983 در ورشو ارائه شد. این جایزه به محققان در زمینه هایی مانند علوم کامپیوتر، زبانهای برنامه نویسی، مدل سازی ریاضیات، محاسبات عددی، بهینه سازی، تئوری اطلاعات، پردازش سیگنال، سیستم های کنترل، هوش مصنوعی و ... ارائه می شود.

RSA Number : اعداد RSA اعداد مرکبی هستند که تنها دو فاکتو اول دارند برای همین گاهی اوقات به آنها اعداد نیمه اول (semiprime) گفته می شود. با وجود آنکه اعداد RSA به مراتب کوچکتر از بزرگترین اعداد اولی است که تاکنون شناخته شده است اما باید اذعان کرد که تجزیه این اعداد در حالی که فاکتورهای آنها اعداد اول بزرگ باشند بسیار بسیار دشوار است. از این اعداد برای سیستم های رمز با کلید خصوصی و عمومی در انتقال اطلاعات استفاده می شود. شرکتی بنام RSA Security جایزه بزرگی به شخصی خواهد داد که الگوریتمی برای تجزیه این اعداد که فقط دو عامل اول بزرگ دارند اعطا خواهد کرد. لازم به ذکر است که تاکنون برای اعداد RSA از 100 الی 174 بیت جوایزی به ارائه دهندگان الگوریتم اعطا شده است اما برای اعداد RSA شامل 193 بیت راه حلی ارائه نشده است.

نسبت طلایی چیست؟

 

 

دنیای اعداد بسیار زیباست و شما می توانید در آن شگفتیهای بسیاری را بیابید. در میان اعداد برخی از آنها اهمیت فوق العاده ای دارند، یکی از این اعداد که سابقه آشنایی بشر با آن به هزاران سال پیش از میلاد میرسد عددی است بنام "نسبت طلایی" یا Golden Ratio.

پاره خطی را در نظر بگیرید و فرض کنید که آنرا بگونه ای تقسیم کنید که نسبت بزرگ به کوچک معادل نسبت کل پاره خط به قسمت بزرگ باشد. به شکل توجه کنید. اگر این معادله ساده یعنی a²=a*b+b² را حل کنیم (کافی است بجای b عدد یک قرار دهیم بعد a را بدست آوریم) به نسبتی معادل تقریبا" 1.61803399 یا 1.618 خواهیم رسید.

شاید باور نکنید اما بسیاری از طراحان و معماران بزرگ برای طراحی محصولات خود امروز از این نسبت طلایی استفاده می کنند. چرا که بنظر میرسد ذهن انسان با این نسبت انس دارد و راحت تر آنرا می پذیرد. این نسبت نه تنها توسط معماران و مهندسان برای طراحی استفاده می شود بلکه در طبیعت نیز کاربردهای بسیاری دارد که به تدریج راجع به آن صحبت خواهیم کرد.

برش اهرام و نسبت طلایی

اهرام مصر یکی از قدیمی ترین ساخته های بشری است که در آن هندسه و ریاضیات بکار رفته شده است. مجموعه اهرام Giza در مصر که قدمت آنها به بیش از 2500 سال پیش از میلاد می رسد یکی از شاهکارهای بشری است که در آن نسبت طلایی بکار رفته است. به این شکل نگاه کنید که در آن بزرگترین هرم از مجموعه اهرام Giza خیلی ساده کشیده شده است.

مثلث قائم الزاویه ای که با نسبت های این هرم شکل گرفته شده باشد به مثلث قائم مصری یا Egyptian Triangle معروف هست و جالب اینجاست که بدانید نسبت وتر به ضلع هم کف هرم معادل با نسبت طلایی یعنی دقیقا" 1.61804 می باشد. این نسبت با عدد طلایی تنها در رقم پنجم اعشار اختلاف دارد یعنی چیزی حدود یک صد هزارم. باز توجه شما را به این نکته جلب می کنیم که اگر معادله فیثاغورث را برای این مثلث قائم الزاویه بنویسم به معادله ای مانند phi²=phi+b² خواهیم رسید که حاصل جواب آن همان عدد معروف طلایی خواهد بود. (معمولا" عدد طلایی را با phi نمایش می دهند)

طول وتر برای هرم واقعی حدود 356 متر و طول ضلع مربع قاعده حدودا" معادل 440 متر می باشد بنابر این نسبت 356 بر 220 (معادل نیم ضلع مربع) برابر با عدد 1.618 خواهد شد.

کپلر (Johannes Kepler 1571-1630) منجم معروف نیز علاقه بسیاری به نسبت طلایی داشت بگونه ای که در یکی از کتابهای خود اینگونه نوشت : "هندسه دارای دو گنج بسیار با اهمیت می باشد که یکی از آنها قضیه فيثاغورث و دومی رابطه تقسیم یک پاره خط با نسبت طلايي می باشد. اولین گنج را می توان به طلا و دومی را به جواهر تشبیه کرد".

تحقیقاتی که کپلر راجع به مثلثی که اضلاع آن به نسبت اضلاع مثلث مصری باشد به حدی بود که امروزه این مثلث به مثلث کپلر نیز معروف می باشد. کپلر پی به روابط بسیار زیبایی میان اجرام آسمانی و این نسبت طلایی برد.

از زیباترین استدلال های یونان قدیم

یکی از زیباترین استدلالهایی که ریاضی دانان یونان پس از شناخت رابطه فیثاغورث و آشنایی با مثلث قائم الزاویه ای که دو ضلع مجاور به وتر آن بطول 1 بود انجام داده اند آن است که "رادیکال دو" (2√) یا همان ریشه دوم عدد 2 نمی تواند یک عدد گویا باشد.

استدلال آنها بسیار ساده بود در نظر می گیریم که ریشه دوم عدد 2 بصورت یک کسر گویا (2√=a/b) بیان شود. همچنین فرض می کنیم که a/b کسر ساده شده می باشد و صورت و مخرج مقسوم علیه مشترک ندارند. در آنصورت اگر طرفین معادله را در خود ضرب کنیم (یا به توان دو برسانیم) باید داشته باشیم : a²/b²=2

بنابراین خواهیم داشت که : a²=2b²

رابطه اخیر نشان می دهد که a² یک عدد زوج می باشد، بسادگی می توان نتیجه گرفت که a نیز باید عدد زوج باشد (چرا؟) ، بنابراین اگر a را بصورت 2t نمایش دهیم خواهیم داشت : 4t²=2b²

اگر معادله بالا را ساده کنیم خواهیم داشت که : b²=2t²

یعنی b هم یک عدد زوج می باشد(چرا؟) ، بنابراین a و b هر دو مقسوم علیه مشترکی مساوی 2 دارند و این مخالف فرضی است که در ابتدا انجام دادیم. بنابراین نمی توان عدد رادیکال دو را بصورت یک کسر گویا نمایش داد.

یک پارادوکس!!!!!!!!!!!!!!!!!!!!!!!!!!!!

سقراط گفته است يوناني ها دروغگو هستند ولي خود سقراط هم يوناني است. پس او دروغ گفته که يوناني ها دروغ مي گويند پس يونانيها راستگو هستند و سقراط هم که يک يوناني است، راستگوست پس راست مي گويد که يونانيها دروغگو هستند پس...........آخر يونانيها دروغگواند يا راستگو!؟

روش کار اراتستن برای محاسبه شعاع زمین

اراتستن سر كتابدار موزه اسكندريه ، نخستين كسي بود كه اندازه زمين را محاسبه كرد . وي متوجه شد كه در ظهر روز تابستاني آفتاب تابستاني ، ستونهاي عمودي در سيرن (اسوان امروز ) هيچ سايه اي نمي اندازد اما همان وقت در اسكندريه در شمال سيرن ستون عمودي عقربه ساعت خورشيدي سايه مي اندازد . با اندازه گيري طول سايه و ارتفاع ستون ، وي تعيين كرد كه فاصله اسكندريه با سمت الراس ، 7.2 درجه است و از آنجايي كه اين رقم حدود يك پنجاهم 360 درجه است پس محيط زمين بايد پنجاه برابر فاصله اسكندريه و سيرن باشد . سپس محيط زمين به دست آمد و به اين ترتيب قطر زمين به دست مي آيد كه فقط 150 كيلومتر با ميزان فعلي تفاوت دارد.

یک معمای جالب!!!!!

در يك مهماني كه من در آن شركت كرده بودم جز من كه فقط با يك نفر ديگر دست دادم هر يك از مهمانان با سه نفر ديگر دست داد. پرسش اول : ايا شما ميتوانيد دست كم تعداد حاضران در اين مهماني را حدس بزنيد؟ پرسش دوم:ايا تعداد شركت كنندگان در اين مهماني ميتواند ۲۱ نفر باشد؟

جواب : دست كم ۶ نفر
اما بيست و يك نفر نميتوانند باشند زيرا 19*3+2=59 كه يك عدد زوج نيست.
اما درباره اينكه چرا نميتوانند بيست و يك نفر باشند.
اگر در شكل فوق مدير را كنار بگذاريم يك گراف خواهيم داشت با پنج گره .گره آبي از درجه دو(فراموش نكنيم كه مدير را كنار گذاشته ايم)و چهار گره سبز از درجه سه،پس مجموع درج هاي گره ها برابر ۳*۴+۲=۱۴ ميباشد.از طرفي مشخص است كه مجموع درجه هاي يك گراف بايد زوج باشد و نميتواند فرد باشد(در اين مثال چون دست دادن يك رابطه دوطرفه است پس مجموع دست دادن ها بايد يك عدد زوج باشد).
حال اگر شمار افراد برابر ۲۱ نفر باشد با كنار گذاشتن مدير بيست نفر خواهيم داشت كه يك نفر با دو نفر دست داده است و ۱۹ نفر با سه نفر دست داده اند كه مجموع دست دادن ها برابر ۲+۳*۱۹=۵۹ ميشود كه بطور روشن غير ممكن است.

 

حدس گلدباخ

در سال ۱۷۴۲ گلدباخ طی نامه ای به اویلر می نویسد: " به نظر می رسد که هر دو عدد زوج بزرگتر از ۲ را بتوان به صورت مجموع دو عدد اول نوشت." این ادعای گلدباخ به حدس گلدباخ شهرت یافت و در این دو نیم قرن اخیر پایه و موضوع تحقیقات گسترده ای شده است.هاروی ریاضیدان برجسته انگلیسی تصریح می کند که حدس گلدباخ یکی از دشوارترین مسائل حل نشده ریاضیات است.

حدس گلدباخ: هر عدد صحیح زوج بزرگتر از ۲ را می توان به صورت مجموع دو عدد اول نوشت.

محاسبات عددی درستی این حدس را نشان می دهند كه به طرق متعددی می توان اعداد زوج را به صورت مجموع دو عدد اول نوشت. در سال ۱۹۷۳ چن نشان داد که اعداد زوج به اندازه کافی بزرگ را می توان به صورت p+m نوشت كه در آن p عددي اول و m عددي اول يا حاصل ضرب دو عدد اول است. گلدباخ حدس زد كه هر عدد فرد بزرگتر از 7 را مي توان به صورت مجموع سه عدد اول نوشت.هر چند كه اين مساله هنوز باز است اما وينوگراف در سال 1937 نشان داد كه همه اعداد فرد مثبت بزرگتر از 3³¹⁵ را مي توان به صورت مجموع سه عدد اول نوشت. اما از لحاظ تئوري نتايج بايد روي همه اعداد فرد مثبت مورد بررسي قرار گيرد.

حالا شما ببينيد مي توانيد به من بگویيد زيبايي حدس گلدباخ در چيست ؟ يا حدس گلدباخ چه اهميتي دارد؟

آشنایی با یک پارادوکس منطقی

به درستی معلوم نیست كه اولین دفعه چه كسی این پارادکس را ابداع كرد، ولی بنا به گفته‌ی کواین - قیلسوف علم مشهور - این مساله قبل از سال 1940 بر سر زبان‌ها افتاده و دهان به دهان می‌گشت و عموماً به صورت  مسأله‌ای تحت عنوان شخص محكوم به مرگ مطرح می‌شد كه اكنون ما به شرح آن می‌پردازیم:

در یك روز جمعه دادگاه شخصی را به مرگ محكوم كرد. قاضی به زندانیِ محكوم گفت:

ظهریكی از روزهای هفته‌ی آینده حكم اعدام درباره‌ی تو اجرا خواهد شد، ولی ما آنروز را برای تو مشخص نخواهیم كرد و تو هرگز قبل از آن روز اطلاع پیدا نخواهی كرد و فقط شش  ساعت قبل یعنی صبحِ روز اجرای حكم موضوع را به تو اطلاع خواهیم داد.

قاضیِ مذكور در همه‌ی عالم به ذكاوت و خوش‌قولی مشهور بود و همیشه دقیقاً به گفته‌ی  خود عمل می‌نمود.

زندانی به همراهی وكیل مدافع خود به سلولش داخل شد و هر دو غمزده در گوشه‌ای به فكر  فرو رفتند. ناگاه وكیل مدافع با لبخندی پیروزمندانه سكوت را شكست و گفت:

اجرای حكم  قاضی امكان ندارد.

زندانی گفت:

من كه چیزی سردر نمی‌آورم. چرا؟

وكیل مدافع پاسخ داد:

اجازه بده تا درست برایت شرح دهم: مسلماًً آن‌ها روز جمعه  نمی‌نتوانند تو را اعدام كنند. به دلیلِ اینكه اگر فرضاً بخواهند در روز جمعه‌ی  آینده حكم را اجرا نمایند. در این صورت تو تمام روزهای هفته و همچنین بعدازظهر  پنج‌شنبه زنده خواهی بود و چون فقط روز جمعه یعنی یك روز دیگر به مهلت باقی مانده، بعد ازظهر پنج‌شنبه برای تو مسلم خواهد شد كه فردا یعنی روز جمعه و تنها روز آخر  هفته ، حكم اجرا خواهد شد. در نتیجه تو روز اجرای حكم را یك روز پیش‌تر پیش‌بینی و  قبل از صبح جمعه از آن اطلاع حاصل كرده‌ای و این موضوع نقض حكم قاضی بوده و گفته‌ی  او را بی‌اعتبار خواهد كرد.

زندانی گفته‌ی او را تصدیق كرد.وكیل مدافع ادامه داد:

بنابراین روز جمعه‌ی آینده از فهرستِ روزهای مهلت حذف و در  آن روز حكم غیرقابل اجرا است. و اما روز پنج‌شنبه نیز نمی‌توانند تو را اعدام كنند  چون در بعدازظهرِ چهارشنبه دو روز بیشتر به آخر هفته نمانده و چون روز جمعه از  فهرست حذف شد ، تنها روز پنج‌شنبه آخرین روز اجرای حكم می‌باشد نتیجتاً بعدازظهر  چهارشنبه تو خواهی دانست در روز پنج‌شنبه كه آخرین روز امكان اجرای حكم است، تو را  اعدام خواهند كرد. اطلاع تو یك روز پیشتر از اجرای حكم مجدداً متناقض با حكم قاضی  است. بنابراین پنج‌شنبه نیز حكم غیرقابل اجرا است. چهارشنبه نیز امكان اجرای حكم  وجود ندارد چون جمعه و پنج‌شنبه حكم غیرقابل اجرا شد و فقط چهارشنبه آخرین روز  اجرای حكم تشخیص داده شد و تو كه بعدازظهر سه‌شنبه هنوز زنده هستی، اجرای حكم روز چهارشنبه را پیش‌بینی خواهی كرد و از آن اطلاع خواهی یافت.

در این موقع كه زندانی از حالت غمزدگی بیرون آمده بود با لبخندی مسرت‌بخش گفت:

پس  به هر طریق می‌توان گفت كه روز سه‌شنبه و سپس دوشنبه و بالاخره یك‌شنبه نمی‌توانند  مرا اعدام كنند و فقط فردا یعنی شنبه باقی است. و اما فردا نیز اجرای حكم برای آنها غیرممكن است چون در این صورت من امروز موضوع را  خواهم فهمید.

ملاحظه می‌شود از لحاظ منطقی هیچ تناقضی در حكم قاضی جهت اعدام زندانی وجود ندارد  با این وجود حكمش غیرقابل اجرا است. به دلایل بالا به نظر می‌آید كه حكم قاضی باعث نقض حكم خودش شده است، اگر حكم را  اجرا كند خلاف حكم خودش شده است، اگر حكم را اجرا كند خلاف حكم خود عمل كرده و اگر  اجرا نكند باز هم خلاف حكم خود رفتار نموده.

روایت دیگری از این پارادکس  از یك اعلامیه‌ی فرمانده‌ی نظامی گفتگو می‌كند كه در آن ذكر شده:

برای تمرین ، در یكی از شبهای هفته‌ی آینده آژیر خطر كشیده خواهد شد. شب تمرین در  شش بعدازظهر همان روز به اطلاع عامه خواهد رسید و تا شش بعدازظهر كسی از شب موعود  مطلع نخواهد شد.

به ظاهر چنین به نظر می رسد که خود این اعلامیه ثابت می‌كند كه تمرین هرگز انجام نخواهد گرفت. به زبان دیگر اجرای تمرین عملی نیست مگر این كه به متن اعلامیه عمل نشود.
نظرِ شما چیست؟

سکه های تقلبی

۱۲ سکه داریم که یکی از آنها تقلبی است(معلوم نیست سنگین تر از بقیه است یا سبکتر) میخواهیم با سه باروزن کردن اون سکه تقلبی رو پیدا کنیم.راه حل شما چيست؟

حل :

12سکه را به 3 دسته 4 تایی تقسیم می کنیم و با انتخاب 2 دسته تا از آنها توزین اول را انجام می دهیم 2 حالت پیش می آید

الف)2 دسته برابرند: پس دسته باقی مانده حاوی سکه تقلبی است. از بین 4 سکه این دسته 2 تا را انتخاب و توزین دوم را انجام می دهیم. اگر برابر بودند سکه تقلبی در بین 2 تای دیگر است، کافی است که یکی از آنها را با یک سکه معمولی بسنجیم(توزین سوم) که سکه تقلبی معلوم می شود. اگر برابرنبودند سکه تقلبی در بین همین 2 تا است، باز کافی است که یکی از آنها را با یک سکه معمولی بسنجیم(توزین سوم) که سکه تقلبی معلوم می شود.

ب) 2 دسته نا برابرند: یکی از 2 دسته حاوی سکه تقلبی است و مساله قدری سخت تراز حالت الف می شود . با خارج کردن 3 سکه از یک دسته و جابجایی 2 سکه از دسته دیگر به این دسته و افزودن 1 سکه معمولی به دسته دیگر توزین دوم را بین 2 دسته 3 تایی ایجاد شده انجام می دهیم .3 حالت پیش می آید

ب-1) دو دسته برابرند پس سکه تقلبی در بین 3 تای خارج شده است. با توجه به اینکه میدانیم از کدام دسته این 3 تا برداشته شده اند نوع نابرابری ان دسته در توزین اول سبکتر یا سنگینتر بودن سکه را معلوم می کند پس با توزین سوم سکه تقلبی بین این 3 سکه معلوم می شود. یعنی 2 تارا با هم می سنجیم اگر برابر بودند سومی تقلبی است واگرنابرابربودند همانی که نوع نابرابری را داشته باشد تقلبی است

ب-2) دو دسته نابرابری خلاف توزین اول دارند پس سکه تقلبی بین 2 سکه جابجا شده است که با توزین سوم معلوم میشود

ب-3) دو دسته نابرابری مشابه توزین اول دارند. پس سکه های خارج شده وسکه های جابجا شده (*) سکه های معمولی هستند و سکه تقلبی بین آنهایی است که جابجا نشده اند. در کل از 8 سکه مشکوک 5 تا کنار میرود و 3 سکه مشکوک باقی میماند. از دسته ای که 2 سکه دارد یکی را خارج می کنیم و1 سکه را به دسته دیگر منتقل می کنیم و در سمت دیگر 2 سکه معمولی می گذاریم توزین سوم را بین این 4 سکه انجام می دهیم .2 حالت پیش می آید:

ب-3-1) دو دسته برابرند پس سکه تقلبی سکه خارج شده است

ب-3-2) دو دسته نابرابری خلاف توزین اول دارند پس سکه جابجا شده همان سکه تقلبی است

ب-3-3) دو دسته نابرابری مشابه توزین اول دارند. پس سکه های خارج شده وجابجا شده سکه های معمولی هستند و سکه غیر این دو تقلبی است

ریاضیات و هنر(3)

 

ریاضیات و هنر (2)

 

ریاضیات وهنر(1)

 

بزرگترین عددی که فقط با سه رقم می توانید بنویسید کدام است ؟

 

 از هیچ کاراکتر و حرفی استفاده نکنید. ( یک تذکر: 999  نیست)

 از هر کسی بخواهید بزرگترین عدد سه رقمی را بنویسد، می گوید  999. جواب منطقی است، اما می توانیم عدد بزرگتری بنویسیم.

 ممکن است کسی موج مغزی قوی دریافت کنه و به  99  به توان  9  فکر کنه، که به شکل زیر محاسبه میشه:

۹۹*۹۹*۹۹*۹۹*۹۹*۹۹*۹۹*۹۹*99  

 حتی  9  به توان  99  بهتر است که ما به صورت  ... ۹*۹*۹*۹  که  99  دفعه تکرار می شود.

 به هر حال، اگر بیشتر فکر کنید جواب صحیح به صورت زیر است:

9  به توان  9  به توان  9.

 اول توانها را حل کنید  (387420489  = ۹*۹*۹*۹*۹*۹*۹*۹*9). با این کار می توانیم عبارت بالا را به شکل  9  به توان  387420489  ساده کنیم، که جواب آن واقعا بزرگ است.

که اصطلاحا به چنین اعدادی " اعداد لی لی پودی" گفته می شود.

در یک صفحه شطرنج چند مربع می توان یافت؟

 

243مربع

 

اثبات

 

پارادوکس مثلثهای همنهشت

 

 

اعداد تاکسی

زماني كه رياضيدان انگليسي هاردي براي عيادت رياضيدان شهير هند رامانوجان به بيمارستان رفته بود به اين موضوع اشاره كرد كه شماره تاكسي كه به وسيله آن به بيمارستان آمده، عدد بي ربط و بي خاصيت 1729 بوده است . رامانوجان بلافاصله ضمن رد ادعاي هاردي به او يادآور شد كه اتفاقا 1729 بسيار جالب توجه است . خود ۱۷۲۹ عدد اول است.

دو عدد ۱۷ و ۲۹ هر كدام عدد اول هستند.
جمع چهار رقم تشكيل دهنده آن ميشود ۱۹ كه اول است.
جمع دو عدد اوليه و دو عدد آخري ميشود ۸۱۱ كه باز هم عدد اول است دو عدد ابتدايي(سمت چپ) اگر جمع شوند؛عدد ۸۲۹ ميشود كه باز هم عدد اول است.
دو عدد اوليه اگر از هم ديگر كسر شوند؛عدد ۶۷ ساخته ميشود كه باز هم عدد اول است. سه عدد سازنده آن عدد اول است(۱و۷و ۲).
عدد اول؛عددي است كه فقط بر يك و خودش تقسيم ميشودبنحوي كه نتيجه تقسيم عددي كسري نباشد(خارج تقسيم نداشته باشد)
جمع عددي اعداد تشكيل دهنده ۱۷۲۹ يا:۱+۷+۲+۹=۱۹ است؛ عكس ۱۹ عدد ۹۱ است؛ اگر ۱۹*۹۱بشودنتيجه برابر ۱۷۲۹ ميشود.
اين هم يكي ديگر از اختصاصات ۱۷۲۹ است كه در هر عددي ديده نميشود.
عدد 1729 اولين عددي است كه مي توان آنرا به دو طريق به صورت حاصلجمع مكعبهاي دو عدد مثبت نوشت :
به توان 3 به علاوه 1 به توان 3 و 10 به توان 3 به علاوه 9 به توان 3 هردو برابر 1729 مي باشند .(اولين مطلب موجود در رابطه با اين خاصيت 1729 به كارهاي بسي رياضيدان فرانسوي قرن هفدهم باز مي گردد.) حال اگر كمي مانند رياضيدانها عمل كنيد بايد به دنبال كوچكترين عددي بگرديد كه به سه طريق مختلف حاصلجمع مكعبهاي دو عدد مثبت است اين عدد87539319 مي باشد كه در سال 1957توسط ليچ كشف شد: 414 به توان 3 + 255 به توان 3 و 423 به توان 3+ 228 به توان 3 و 436 به توان 3 + 167 به توان 3 هر سه جوابشان برابر 87539319 است .

امروزه رياضيدانان عددي را كه به n طريق مختلف به صورت حاصلجمع مكعبهاي دو عدد مثبت باشد ،n ــامين عدد تاكسي مي نامند و آنرا با Taxicab نمايش مي دهند.جالبتر از همه اينكه ،هاردي و رايت ثابت كردند براي هر عدد طبيعي n ناكوچكتر از 1 ،n ــامين عدد تاكسي وجود دارد !

هرچند، چهارمين تا هشتمين اعداد تاكسي نيز كشف شده اند ولي تلاشها براي يافتن نهمين عدد تاكسي تاكنون نا كام مانده است . متاسفانه اطلاعات زيادي درباره اعداد تاكسي موجود نيست . در ضمن ميتوان مسئله را از راههاي ديگر نيز گسترش داد . مثلا همانگونه كه هاردي در ادامه داستان فوق از رامانو جان پرسيد و او قادر به پاسخگويي نبود ، اين پرسش را مطرح كنيد: كوچكترين عددي كه به دوطريق حاصلجمع توانهاي چهارم دو عدد مثبت مي باشد ،كدام است؟ اين عدد توسط اويلر يافت شده است :635318657 حاصلجمع توان چهارم 59 و 158 همچنين توانهاي چهارم 133 و 134 مي باشد.

 

آمار گیری

- یه آمار گیر میره در یه خونه ای و راجع به خودش و بچه هاش سوال میکنه.

طرف میگه: "برای سن بچه هام یه معما میگم باید حلش کنی تا سنشون رو پیدا کنی. من سه پسر دارم که حاصل ضرب سن اونا میشه 36 و حاصل جمع سنشون 2 تا از شماره پلاک همسایه سمت راستی کمتره".

آمار گیره یه خورده فکر میکنه و میگه: "با این اطلاعات نمیتونم حلش کنم میشه یه راهنمایی بکنین".

صابخونه میگه: "پسر بزرگترم حلوا شکری عقاب خیلی دوست داره!!!" و آمارگیره مساله رو حل میکنه.

 حالا شما میتونین بگین سن بچه ها به ترتیب چند بوده؟

اگه اعدادی که حاصل ضربشون میشه 36 رو بنویسین میشه این لیست:
1  1  36 -> که حاصل جمعشون میشه 38
1  2  18 -> 21
1  3  12 -> 16
1  4  9  -> 14
1  6  6  -> 13  *
2  2  9  -> 13  *
2  3  6  -> 11
3  3  4  -> 10

آمارگیر پلاک خونه همسایه رو میدیده ولی گفته با این اطلاعات نمیتونه حلش کنه. پس حتما ابهامی تو قضیه بوده و این ابهام تنها از دو سری 1 6 6 و 2 2 9  ناشی میشه که جمع هر دو 13 میشه. حالا از این که صابخونه گفته "پسر بزرگترم" میتونیم نتیجه بگیریم که از بین پسراش یه پسری باید سنش از همه بیشتر باشه و یعنی دوقلو نداشته باشه. پس جواب میشه 2 2 9.
 به جای حلوا شکری عقاب هم هر چیز دیگه ای میتونه باشه. 

 

مساله انشتین

-  این مساله را انشتین در قرن نوزدهم مطرح کرده  و گفته است 98 درصد مردم دنیا قادر به حلش نیست. ممکن است ظاهر مساله خسته کننده باشد ولی در باطن نیست:

1- در یک خیابون 5 خانه وجود دارد که با پنج رنگ متفاوت رنگ شدند.
2- در هر خانه يک نفر با ملیت متفاوت با بقیه زندگی میکند.
3- هر کدوم از 5 صاحبخونه يک نوشیدنی متفاوت, یه مارک سیگار متفاوت دوست دارد و يک حیوان متفاوت در خانه نگهداری میکند

سوال این است که چه کسی در خانه ماهی نگهداری میکنه با این شرطها که:

1- انگلیسه خونه اش قرمزه
2- سوئدیه تو خونه سگ نگه میداره
3- دانمارکیه چای دوست داره
4- خونه سبز رنگ سمت چپ خونه سفیده
5- صاحب خونه ی سبز رنگ قهوه دوست داره
6- کسی که سیگار پالمال میکشه پرنده نگهداری میکنه
7- صاحب خونه زرد رنگ سیگار دانهیل میکشه
8- مردی که تو خونه وسطی زندگی میکنه شیر دوست داره از نوشیدنی ها(نه حیوونا)
9- نروژیه تو اولین خونه زندگی میکنه
10- مردی که بلندز میکشه همسایه اونیه که گربه نگهداری میکنه
11- مردی که اسب نگهداری میکنه همسایه مردیه که دانهیل میکشه
12- مردی که بلو مستر میکشه آبجو دوست داره(ببخشید ماءالشعیر)
13- آلمانیه سیگار پرنس میکشه
14- نروژیه همسایه اونیه که خونه اش آبیه
15- مردی که بلندز میکشه همسایه ای داره که آب دوست داره بین نوشیدنیها

حالا نگین زمان انیشتین این سیگارها نبوده. لابد یه بدبختی اومده به جای ایکس و ایگرگ  این چیزها رو گذاشته که مساله طبیعی تر بشه.

مرد زرنگ و جوان ساده دل

مردي تردست كه با جواني ساده دل اما ازمند همسفر شده بود و به مقدار پولش
پي برده بود به او چنين پيشنهادي كرد:
تردست:دوست داري پولت را دو برابر كنم؟؟
ساده دل:چه بهتر از اين.
تر دست:يك شرط دارد هر بار كه پولت را دو برابر كنم بايد 800 تومان به من بدهي
قبول ميكني؟؟
ساده دل شرط را پذيرفت اما پس از 3 بار همه ي پولهايش را از دست داد!!
اين جوان ساده دل قبل از اين شرط بندي چند تومان با خود داشته است؟؟

**جوان در بار سوم كه پس از دو برابر شدن پولش و پرداختن 800 تومان چيزي
برايش نمانده 400 تومان داشته است
بار دوم پس از دو برابر شدن پولش 1200=800+400 تومان و پيش از ان 600=2/1200 تومان داشته است .
به همين ترتيب معلوم ميشود كه پولش در بار نخست برابر بوده با:
700=2/(600+800).................700 تومان

یک عدد عجیب!!!!

یک نفر از اساتید دانشکده شهر آتن پایتخت یونان چندی پیش عددی را کشف کرد که خصایص عجیبی دارد.
آن عدد:142857 میباشد.
اگر عدد مذکور را در دو ضرب کنیم، حاصل: 285714 میشود! (به ارزش مکانی 14 توجه کنید).
اگر این عدد را در سه ضرب کنیم حاصل: 428571 میشود!(به ارزش مکانی 1 توجه کنید).
اگر این عدد را در چهار ضرب کنیم حاصل: 571428 میشود!( به ارزش مکانی 57 توجه کنید).
اگر این عدد را در پنج ضرب کنیم حاصل: 714285 میشود!(به ارزش مکانی 7 توجه کنید).
اگر این عدد را در شش ضرب کنیم حاصل: 857142 میشود! (سه رقم اول با سه رقم دوم جا بجا شده)
اگر این عدد را در هفت ضرب کنیم حاصل: 999999 میشود!
لطفا" ضربهای بالا را خود شما نیز انجام دهید و حاصل را با عدد اصلی مقایسه کنید

چهل و یکمین عدد مرسن شناخته شد.

پس از گذشت کمتر از شش ماه از اکتشاف چهلمین عدد اول مرسن عدد
با 7,235,733 رقم نه تنها به عنوان بزرگترین عدد اول مرسن شناخته شده بلکه به عنوان بزرگترین عدد اولی که تا کنون کشف شده است شناخته شد. طبق گزارشی که در سایت "کشف اینترنتی اعداد اول مرسن" (GIMPS) ارائه شد این عدد از الگوریتم "لوکاس- لمر" با موفقیت عبور کرده و در نتیجه عددی اول می باشد.
بزرگترین هفت عدد اول مرسن از جمله آخرین آنها توسط یک همکاری بین المللی به وسیله داوطلبان GIMPS کشف شده اند. آخرین عدد اول مرسن کشف شده توسط یکی از داوطلبان GIMPS به نام "جاش فیندلی" پس محاسباتی دو هفته ای با کامپیوتر P4 2.4GH شناخته شده است این نتیجه به طور جدا گانه توسط "تونی ریکس" و "جف گیلچریس" پس از محاسباتی که به ترتیب 5 و 11 روز به طول انجامیده است تأیید شد.
الگوریتمی که برای تست اول بودن یک عدد در GIMPS مورد استفاده قرار می گیرد توسط دکتر "ریچارد کرندل" - مدیر مرکز محاسبات پیشرفته در کالج رید در ارگون پورتلند - به وسیله نرم افزار Mathematica تهیه شده است.

جالب و خواندنی

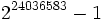
چرا 14 مارس روز عد پی نامگذاری شده است؟

این نامگذاری به علت سه رقم اول عدد پی ( یعنی ۱۴/۳)میباشد.یعنی روز چهاردهم از سومین ماه میلادی،البته بد نیست بدانیم آلبرت انیشتین هم در این روز چشم به جهان گشود.

جادوی اعداد

اگر از كوچه پس كوچه‌هاي قديمي شهرآنجايي كه هنوز رگه‌هايي از خانه‌هاي قديمي كاهگلي يافت مي‌شود گذر كنيم هنوز هم پلاكهاي خانه‌هايي را مي توان ديد كه روي آن 1+12  به جاي سيزده نوشته شده است، علت آن را در اعتقادات مردم مي توان يافت تحت اين عنوان: نحس بودن 13 !
آنچه در ادامه خواهيد خواند جادوي 13 است كه به نظر جالب مي رسد !!!

  

● 13 عدد اول است.     

● 1-13^2  عدد اول مرسن است.

● 13جسم ارشميدسي موجود است. (اجسام ارشميدسي اجسامي هستند كه وجوه آنها چند ضلعي بوده، نه لزوما از يك نوع ، و كنجهاي آنها مساوي هستند.)
 

● عدد 13كوچكترين Emirp است. (Emirp  عدد اولي است كه اگر ارقام آن را معكوس كنيم مجددا عددي اول خواهد بود مثلا اعداد 13، 17،31، 37،.....)

● 169=2^13  بامعكوس كردن ارقام آن داريم: 961="2^31 يعني رقم هاي آن مجددا معكوس مي شود."

●2^13،  1+!12 را عاد مي‌كند.

● 13عدد Happy است.(براي دانستن اين كه عددي Happy است، مجموع مربعات رقمهاي عدد را پيدا كرده و دوباره مجموع مربعات عدد بدست آمده را حساب مي‌كنيم با ادامه اين روند اگر به عدد 1 دست پيدا كرديم آنگاه به آن عدد Happy گفته مي‌شود. مثلا براي عدد سيزده  10="2^3+2^1 و 1=2^0+2^1 بنابراين13" عدد Happyاست.)

● 13نيمي از  3^3+ 3^1- است.
 

●شاخه زيتوني كه در پشت دلارهاي آمريكا كشيده شده است 13 برگ دارد.

●2^13عدد !(1 -13)+ 1را عاد مي‌كند بنابراين يك عدد اول ويلسون(Wilson Prime) است. ( هر عدد اول p كه،p و p^2،  مقدار p-1)!+1 ) را عاد كنند، عدد اول ويلسون ناميده مي‌شود. مثلا  عدد 5 عدد ويلسون است.  تنها اعداد شناخته شده 5  و 13و 563 است .)

●چرتكه چيني داراي  سيزده ستون مهره‌ براي محاسبات است.

●  13بزرگترين عدد اولي است كه مي تواند به دو عدد متوالي به صورت n^2+3 افراز مي شود.

 ● 1+13- 13^13 عدد اول است.

 ● نخستين حفره‌ي اول با طول سيزده بين دو عدد    113و 127اتفاق مي‌افتد. (منظور از حفره‌ي اول تعداد  اعداد مركب بين دوعدد اول متوالی است.)  

 

 ● 13 كوچكترين عدد اول جايگشت‌پذير (Permutable Number) است. ( اين اعداد، اعداد اولي  حداقل با دو رقم مجزا هستند  كه با تجديد آرايش در رقم هايشان همچنان عددي اول باقي مي مانند مثلا براي عدد 337  ، 733 و 373 و 337 عدد اول است از ديگر اعداد از اين قسم مي‌توان به  13,17,37,79,113,119و جايگشتهاي آن اشاره كرد.)

● هشت عدد اول ديگر مي‌تواند به وسيله تغيير يك رقم از 13 توليد شود.{11, 17, 19, 23, 43, 53, 73, 83}

● نخستين بار پرچم امريكا 13 ستاره و 13 خط داشت كه نشان دهنده تعداد مستعمرات اصلي اين كشور بود.

● عدد 13 كوچكترين عددي است كه ارقام آن در پايه چهار معكوس 13 است. ( 13 در پايه چهار 31 است.)

● رويه‌ي بيضوي روي اعداد گويا كه داراي نقطه‌ي گويا از مرتبه‌ي 13 باشد موجود نيست.

● 2^13= 19+...+8+7

● عدد 2^13توسط مربعات مجزاي اعداد 1 و 2 و 3 و 4 و 5 و 6 بيان مي‌شود.

●طولاني ترين ركورد پرواز يك جوجه 13 ثانيه است.

 

●131211109876543212345678910111213عدد اول است.

● معكوس عدد 2^13 عددي اول است.

● ELEVEN + TWO = TWELVE + ONE(عبارت فوق تحريفي از حل معادله‌ي 13 است.)

● 13كوچكترين عدد اولي است كه از مجموع مربعات دو عدد اول مجزا يعني 2^3+2^2 بدست مي آيد.

●اقليدس و ديافانتي هر كدام 13 كتاب نوشته‌اند.

●با به كار بردن نخستين سه عدد اول داريم : 13="5+3^2

●فيلم" 13 نوامبر" ، آلفرد هيچكاك  هيچگاه به پايان نرسيد.

● بعضي از افراد فكر مي كنند كه عدد 13 عددي نحس است.

●مجموع  نخستين 13عداد اول  برابر 13 امين عدد اول است.

●رساله 13 جلدي Almagestبزرگترين كار بطلميوس بود.  قضيه‌ي رياضي را با توجه به حركتهاي ماه ،خورشيد و سياره ها را فراهم ساخت.

● مجموع باقي مانده هاي حاصل از تقسيم عدد 13 برنخستين اعداد اول تا 13 برابر 13 است.

●  13كوچكترين عدد اولي است كه مجموع ارقام آن مربع است.

●13كوچكترين عدد اولي است كه به شكل p^2+4(  كه p اول است) نوشته مي شود.

● اويلر 13 فرزند داشت كه 5 فرزند او به سن نوجواني رسيدن و تنها 3 نفر باقي ماندند.

● مجموع توانهاي چهارم نخستين 13عدد اول به علاوه‌ي عدد يك ، عددي اول(6870733) است.

● 13  كوچكترين عدد اول Sextanاست اين عدد برابر است با : 
(p = (x^6+y^6)/(x^2+ y^2

● اگر براي عدد اول pداشته باشيم:p-1)!="-1   " mod p^2 )    آن عدد، عدد ويلسون است. ( تنها اعداد شناخته شده 5 ،13 و 563 است.)

● (13+1)13-13^(13+1) عددي اول است.

● بد يمن بودن روز جممعه ايي كه 13امين  روز ماه باشد يكي از خرافات رايج در جوامع است.

●13كوچكترين عدد اولي است كه به صورت مجموع مجزا از اعداد اول به شكل 4n+3نيست.

●به طور طعنه آميز گفته مي شود كه : 13 ، 15 امين عدد خوشبختي است.

●13بزرگترين عدد اول فبوناچي است كه(13)Fاول است.

●13 از متصل شدن دو عدد نخست مثلثي ساخته مي‌شود.( 1, 1+2, 1+2+3 ...  اعداد مثلثي هستند.)

 
● مجموع نخستين 13 عدد اول 238كه مجموع ارقامش 13 است.

 
● .به طور طبيعي هر سال 12 ماه دارد اما در حقيقت 13 ماه داريم تعجب نكنيد ماه آسمان را فراموش كرديد با دوازده ماه سال 13 مي شود.

 
● 13="2^3+1^3+0^3 

 
●  كوچكترين عدد اولي است كه به صورت مجموع دو عدد اول ( 2+11) نمايش داده مي‌شود و همچنين كوچترين عدد اولي است كه به صورت مجموع دو عدد مركب (4+9 ) نوشته مي‌شود.

 
● 13بزرگترين عدد اول مينيمال در پاي 3 است.

 
● 13/13333333333333 عدد اول است. (توجه كنيد كه تعداد ارقام 3 بعد 1 ، 13 عدد است.)

● 13="3+7+3(توجه" كنيد كه3^13="(7+3)+7^3)

● 0^10+2^10+3^10+5^10+7^10+11^10+13^10عدد" اول است كه بزرگترين عدد اول نا تيتانيك (Titanic Number) است. ( NumberTitanicاعداد اولي هستند كه تعداد ارقام آن بيشتر از 1000 است.)

● 13-13^2عدد اول است.

● 13+13+13/13+13*13+!13+13^13 و13+13+13/13+13*13+13^13  دو عدد پانزده رقمي اول هستند.

● 13جوابي براي معادله‌ي ديوفانتوسي (Diophantine Equation)  z^2="x^3-y^3" است. يعني؛ 3^7-3^8="2^13

● 13/(13+13+13+13+13+13+13+131313+13^13) عددي اول است كه شامل 13بار تركيباتي از عدد 13 است مثلا 131313سه بار 13 در آن آمده است.

● ماموريت قمر" آپولو 13" در مسير ماه بي نتيجه ماند علت انفجار در قسمتي از سفينه بود . نكته جالب اين است كه اين قمر در ساعت 13:13  پرتاب شده بود  و اين اتفاق در 13 اوريل شكل گرفت. ( احتمالا روز جمعه!!!!!!!!)

● 13امين عدد اول مرسن عدد 1-521^2 و 13امين عدد لوكاس (Lucas Number) عدد521است.)اعداد لوكاس اعدادي هستند كه به نام رياضيدان فرانسوي     EdouardLucasنامگذاري شده اند و در دنباله 1 و3و4و7 و11و.... قرار دارند اين دنباله به صورت ذيل ساخته مي شود كه جمله اول 1 و دومين جمله 3 جمله هاي بعدي از مجموع دو جمله قبلي ساخته مي شود مثلا جمله سوم مجموع جمله اول با دوم يعني 1+3 است.

● (13="(!3*!1)+(!3+!1)13" و 31تنها اعداد مرسن Emirp   شناخته شده هستد.

 
● 13كوچكترين عدد اولي است كه به شكل p^2+pq+p   نوشته مي‌شود.

 
● معكوس ((1+13^13)^13) يك عدد Brilliantاست. ( به اعدادي Brilliantگويند كه دو فاكتور اول با طول يكسان دارند.)

پارادوکس حرکت

پارادوکس حرکت!!

يک روز زنون از اهالی الئا يکی از فلاسفه بزرک يونان که شيفته پارادوکسها بود اعلام کرد :(( حرکت غير ممکن است. )) او استدلال کرد برای به هدف رسيدن يک پيکان, ان پيکان ابتدا بايد نصف مسافت را طی کند, سپس نصف مسافت باقيمانده را به همين صورت تا اخر;به طوری که به نظر ميرسد پيکان هرگز به هدف نخواهد رسيد(قضيه limit ).اما در واقع از انجا که مسافتها کوچکتر پی در پی کوتاهتر ميرسد به اين نتيجه ميرسيم که پيکان به هدف خواهد رسيد. 

 

حل یک مسئله ریاضی توسط دو تن از دانشمندان ایرانی

با تلاش دو دانشمند ایرانی یکی از مسائل ریاضی پس از 20 سال تلاش ناموفق ریاضیدانان جهان حل شد

محققان پژوهشكده رياضيات پژوهشگاه دانش‌هاي بنيادي با ساخت «ماتريس آدامار از مرتبه 428 » به 20 سال تلاش ناموفق رياضيدانان جهان در اين زمينه پايان دادند. به گزارش بخش خبر سایت اخبار فن آوری اطلاعات ایران، به نقل از ایسنا، اين موفقيت علمي كه با تلاش دكتر هادي خرقاني، استاد دانشگاه « لث بريج » كانادا و محقق ميهمان پژوهشگاه دانش‌هاي بنيادي و دكتر بهروز طايفه رضايي، عضو هيات علمي پژوهشگاه حاصل شده، بازتاب قابل ملاحظه‌اي در محافل علمي رشته «تركيبيات» داشته و در برخي از وب سايت‌هاي معتبر اين رشته انعكاس يافته است. دكتر طايفه رضايي در این گفت‌و‌گو اظهار داشت: محاسبات مربوط به ساخت «ماتريس آدامار از مرتبه 428‌» با استفاده از يك شبكه محاسباتي شامل 16 رايانه شخصي 6/2 گيگاهرتز در مدت حدود 12 ساعت - كه از لحاظ مدت زمان كوتاه نيز در نوع خود ركوردي محسوب مي‌شود - انجام شده و بدين ترتيب علاوه بر اين ماتريس، تعداد زيادي ماتريس آدامار ديگر نيز كه پيش از اين نامعلوم بوده‌اند، ساخته شده‌اند. وي با اشاره به اينكه يكي از گروه‌هاي تحقيقاتي اروپايي با وجود سه سال تلاش بي‌وقفه با بهره‌گيري از تعداد بيشتري رايانه موفق به ساخت اين ماتريس نشده‌ بود، خاطرنشان كرد: ما با دستيابي به روش‌هايي جديد، محاسبات پيچيده ساخت ماتريس را كاهش داده و توانستيم در مدتي كوتاه به اين ماتريس دست يابيم. عضو هيات علمي پژوهشگاه دانش‌هاي ‌بنيادي تصريح كرد: ماتريس‌هاي آدامار يكي از زمينه‌هاي مهم تحقيق در«تركيبيات» است كه در سال‌هاي پس از جنگ جهاني دوم مورد استفاده عملي فراواني پيدا كرده‌اند. يكي از موارد استفاده جالب اين ماتريس‌ها در كدگذاري تصاويري است كه توسط سفينه‌ها از ساير سيارات ارسال مي‌شود. اين ماتريس‌ها همچنين در زمينه‌هايي همچون نظريه رمزنگاري، پردازش سيگنال‌ها، نظريه طرح‌ها و آزمايش‌هاي آماري كابرد دارند. وي افزود: كوچكترين ماتريس آدامار ناشناخته دردهه 70 ازمرتبه 268 بود كه درسال 1985، اين ماتريس ساخته شد و بدين ترتيب ماتريس‌هاي آدامار از مرتبه‌هاي كوچكتر از 428 معلوم شدند. با ساخت ماتريس آدامار از مرتبه 428، كه پس از دو دهه تلاش ناموفق گروه‌هاي متعدد تحقيقاتي در نقاط مختلف دنيا حاصل شده كوچكترين ماتريس آدامار نامعلوم از مرتبه 668 است. دكتر طايفه رضايي در پايان خاطرنشان كرد: با دستيابي به اين ماتريس، مساله وجود ماتريس‌هاي آدامار با هر مضرب 4 كه به «حدس آدامار» معروف است، تقويت مي‌شود.

بی نهایت یعنی؟؟؟

بی نهایت از واژه لاتین "finitus" به معنی "محدود" گرفته شده ) علامت ( ∞ چیزی است که "محدود" نیست، که در آن هیچ محدودیتی زمانی و فضایی وجود ندارد.

نگرش باستانی در مورد بی نهایت

نگرش باستانی از ارسطو آغاز شده است:

“... تفکر درباره یک عدد بزرگ همیشه ممکن است: چون تعداد دفعاتی که میتوان یک مقدار را به دو نیمه تقسیم کرد، بی نهایت است. بنابراین بی نهایت، امکان بالقوهای است که هرگز بالفعل نمی گردد؛ تعداد اجزایی را که می توان به دست آورد، همیشه از هر عدد معینی بیشتر است.

به این مورد اغلب بی نهایت "بالقوه" اطلاق می شود، بهرحال دو نظریه در این مورد با هم ترکیب شده اند. یکی اینکه همیشه پیدا کردن چیزی هایی که تعداد آنها از هر عددی بیشتر باشد ممکن است، اگرچه آن چیزها عملا وجود نداشته باشند. دیگر اینکه ما می توانیم بدون محدودیتی، اعداد بالاتر از محدود را شمارش کنیم. مثلا "برای هر عدد صحیح n، یک عدد صحیح m (m > n) وجود دارد .دومین نگرش را بصورت واضح تر در آثار نویسندگان قرون وسطایی مثل William of Ockham میتوان یافت:

:"Sed omne continuum est actualiter existens. Igitur quaelibet pars sua est vere existens in rerum natura. Sed partes continui sunt infinitae quia non tot quin plures, igitur partes infinitae sunt actualiter existentes."
):هر زنجیره حقیقتا وجود دارد. بنابراین هر یک از اجزاء آن واقعا در طبیعت وجود دارد. اما اجزاء زنجیره نامحدود هستند چون هیچ عدد بزرگی نیست که عددی بزرگتر از آن نباشد، پس اجزاء نامحدود واقعا وجود دارند.)

اجزاء از بعضی جهات واقعا وجود دارند. بهرحال، در این نگرش، هیچ بزرگی بی نهایتی نمی تواند یک عدد داشته باشد، چون هر عددی را که تصور کنیم، همیشه عددی بزرگتر از آن وجود دارد: "هیچ بزرگی (از لحاظ عددی) نیست که بزرگتر از آن نباشد". Aquinas همچنین بر ضد این نظریه که بی نهایت می تواند از هر جهت کامل یا کلی باشد بحث کرده است .

نگر ش های نوین آغازین

گالیله در زمان بازداشت طولانی در خانه اش در Sienna بعد از محکومیتش توسط استنطاق مذهبی اولین کسی بود که متوجه شد می توان مجموعه ای از بی نهایت عدد را بصورت تناظر یک به یک با یکی از زیر مجموعه های حقیقی آن در کنار هم قرارداد.
با این استدلال مشخص می شود، اگرچه طبیعتا یک مجموعه که بخشی از مجموعه دیگر بوده، کوچکتر است(چون تمام اعضاء آن مجموعه را شامل نمی شود) از بعضی جهات هم اندازه اند. او معتقد بود این یکی از مشکلاتی است که وقتی ما میخواهیم "با ذهن محدود خود" یک امر نامحدود را درک کنیم، پیش می آید.

ادراک ریاضی

درک ریاضی مدرن از بینهایت در اواخر قرن نوزدهم توسط کارهایGeorg Cantor،
Gottlob Frege، Richard Dedekind] و دیگران با استفاده از ایده مجموعه ها، توسعه یافت.برخورد آنها در اصل به قبول ایده ««تناظر یک به یک بعنوان یک استاندارد برای مقایسه سایز مجموعه ها بود، و رد کردن نظر گالیله (که از اقلیدس ناشی شده بود) مبنی بر اینکه کل نمیتواند هم اندازه جزء باشد. یک مجموعه نامحدود را میتوان بصورت ساده طوری تعریف نمود که هم اندازه حداقل یکی از اجزاء "مناسب" آن باشد.

بدینسان کانتور نشان داد که مجموعه های بینهایت میتوانند اندازه های متفاوت داشته باشند، با تمایز بین مجموعه های بینهایت قابل شمارش و بینهایت غیر قابل شمارش، و یک فرضیه اعداد کاردینال را حول این مطلب توسعه داد. نظر او غالب گردید و ریاضیات مدرن عملا بینهایت را پذیرفت. سیستمهای اعداد توسعه یافته مشخصی، مانند اعداد حقیقی، اعداد معمولی(محدود) و اعداد نامحدود را با سایزهای مختلف، متحد می نمایند.

وقتی سروکارمان با مجموعه های نامحدود می افتد، بصیرت کسب شده ما از مجموعه های محدود ازکار میافتد. یک مثال برای این پارادوکس گراند هتل هیلبرت است.

یک سوال فریبکارانه این است که آیا بینهایت عملی در کیهان مادی وجود دارد: آیا تعداد ستاره ها نامحدود است؟ آیا کیهان دارای حجم نامحدود است؟ آیا فضا "تا ابد ادامه" دارد؟ این یک سوال باز مهم در کیهان شناسی است. توجه داشته باشید که سوال از نامحدود بودن بصورت منطقی، غیر از سوال در مورد داشتن مرز می باشد. سطح دو بعدی زمین، برای مثال، محدود است، در حالیکه هیج مرزی ندارد. با راه رفتن / دریانوردی / رانندگی به اندازه کافی طولانی در مسیر مستقیم، شما درست به همان نقطهای که شروع کرده بودید، باز می گردید. کیهان، حداقل در مبادی و اصول، ممکن است بر اساس یک اصل مشابه عمل نماید؛ اگر شما با فضاپیمای خود به اندازه کافی طولانی در مسیر مستقیم و روبروی خود پرواز کنید، شما اتفاقا و بصورت ناگهانی دوباره از همان نقطهای که از آن شروع کرده بودید، می گذرید.

نظریات مدرن

مباحث مدرن درباره بینهایت امروزه بصورت بخشی از تئوری مجموعه و ریاضیات مرد توجه قرار گرفته است، و کلا فلاسفه از بحث درباره آن احتراز می کنند Wittgenstein .یک استثناء بوده است، کسی که حملات مهیجی را علیه بدیهیات تئوری مجموعه، و ایده بینهایت عملی، در "اواسط عمر خود" انجام داد.

بینهایت امروزه به انواع مجوعه های نامحدود زیادی تقسیم شده است، مانند aleph-null، یک سری قابل شمارش از اعداد طبیعی، و beth-one، یک سری غیر قابل شمارش مانند تعداد کمانهای موجود در یک دایره یا تعداد نقاط روی یک خط، و یک تعداد نامحدود از چیزهای دیگر.

:"آیا معادله m = 2n گروه تمام اعداد را با زیرگروههایش مرتبط می کند؟ خیر. آن هر عدد دلخواهی را با دیگری مرتبط می سازد، و بدین ترتیب ما به گروههای زوج نامحدود وارد می شویم، که هرکدام به دیگری مرتبط میباشد، ولی هرگز به گروه یا زیرگروهی مرتبط نیستند. هیچیک از این دو، یکجوری خودش یا دیگر گونه از یک زوج گروه، فرآیند نامحدود نمی باشند ... در موهومات که m = 2n یک گروه را با زیرگروههایش مرتبط می سازد، هنوز ما صرفا یک حالت از دستور زبان دوپهلو را خواهیم داشت." (Philosophical Remarks ? 141, cf Philosophical Grammar p.465)

مطلق

سوال دیگر این است که آیا ادراک ریاضی از بینهایت ارتباطی با ادراک مذهبی از خدا دارد؟ این سوال هم کانتور را، با عقیده اش در مورد بینهایت مطلق که با خدا برابر قرارداده شده است، و هم Kurt Godel را با اثبات ؟؟؟ Godel's ontologicalاش از وجود یک نهاد که او آنرا به خدا وابسته کرد، مخاطب خود قرار داده است.

یک کاغذ را چند بار می توان تا کرد؟

شايد تا کنون شده باشد که در مواقعی که بيکار هستيد يا اينکه انتظار خبر مهمی را می کشيد برای سرگرم کردن خودتان کاغذی را که در اطرافتان هست برداريد و شروع به تا کردن آن  کنيد و بعد از چند بار متوجه شويد که ديگر نمی شود کاغذ را تا کرد. در اين صورت يا از تا کردن کاغذ منصرف می شويد يا آن را باز می کنيد و دوباره شروع به تا کردنش می کنيد... البته ممکن است قبل از اينکه به آن زمان برسيدخبر مهم به شما داده شود  و کاغذ را به جای اولش برگردانيد !!!

     اين مسئله را همه ما تجربه کرده ايم اما شايد هيچ کدام از ما به طور جدی روی آن فکر نکرده باشيم.

     اگر ورق را هر بار طوری تا کنيد که اندازه آن نصف شود بيش از ۷ يا ۸ بار نمی توانيد آن را تا کنيد. مهم نيست ورق اوليه شما چقدر بزرگ باشد. شايد تا به حال اين قضيه را شنيده باشيد و سعی کرده باشيد که آن را امتحان کنيد و متوجه شده باشيد که تا کردن کاغذ بيش از۷ يا ۸ بار بسيار سخت است. آيا می توان گفت که اين اعداد يک محدوديت مستدل و عمومی برای تا کردن کاغذ هستند؟

فرض کنید شما کاغذی را انتخاب کرده ايد که دارای پهنای w و ضخامت t است . اگر شما شروع به تا کردن ورق از يک سمت بکنيد وقتی به جايی برسيد که ديگر نتوانيد کاغذ را تا کنيد يک نوار باريک خواهيد داشت.

با هر تا کردن ضخامت کاغذ دو برابر می شود و پهنای آن نصف خواهد شد. يعنی بعد از N بار تا کردن ضخامت 2ⁿ خواهد بود و البته مشخص است که پهنا ۰.۵ⁿ  می شود

اگر با کاغذی به پهنای 11cm و ضخامت 0.002cm اين کار را انجام دهيد بعد از 7 بار تا کردن نسبت t/w برابر 1/6 می شود. اين بدان معنيست که اندازه ضخامت از پهنا بيشتر می شود و در نتيجه ديگر قادر به تا کردن کاغذ نخواهيد بود. اگر اين کاغذ را 50 بار بزرگتر کنيد شايد بتوانيد آن را تا ۱۰ بار هم تا کنيد.

اگر به صورت متناوب کاغذ را از عرض و طول تا کنيد ممکن است تعداد دفعات بيشتری بتوانيد به تا کردن کاغذ ادامه دهيد. در اين صورت هر بارضخامت دو برابر می شود در صورتی که پهنا هر دو دفعه يک بار نصف می شود.

چندين سال پيش هنگامی که بريتنی گاليوان در دبيرستان درس می خواند با اين مسئله رو به رو شد که چگونه کاغذی را ۱۲ بار تا کند . او بايد برای گرفتن نمره از يکی از کلاسهايش اين مسئله را حل می کرد. بعد از آزمايش راه های مختلف او موفق شد که ورقه نازکی از طلا را ۱۲ بار تا کند. اما مسئله طرح شده در باره کاغذ بود و نه طلا.

گاليوان بر روی معادله تعداد دفعاتی که می توان يک کاغذ با اندازه معين را تا کرد کار کرد.

 

که در آن L کمترين درازای کاغذ، t ميزان ضخامت کاغذ و n تعداد دفعاتی است که می توان کاغذ را تا کرد. واحد t و L بايد يکسان باشد.

براي يک طول و ضخامت معين عبارت *******بيانگر آن است که صفحه بعد از n بار تا کردن چند برابر کوچک شده است. با n=0 شروع می کنیم و به همين ترتيب به رشته ای از اعداد به اين صورت می رسيم:

0, 1, 4, 14, 50, 186, 714, 2794, 11050, 43946, 175274, 700074, 2798250, . . .

اين به اين معنی است که در تای دوازدهم 2798250 برابر مقدار کاغذی که در تای اول از دست می رود از دست خواهد رفت.

گاليوان در کتابی با نام ((Historical Society of Pomona Valley)) چگونگی به دست آوردن اين معادله و تلاشش برای حل مشکل را توضيح داده است. بالاخره در June 2002 گاليوان يک کاغذ بزرگ را ۱۲بار تا کرد.

راستی اگر از دید دیگری مسئله را نگاه کنیم باز هم جالب خواهد بود. منظورم این است که اگر تا کردن کاغذ را با ارتفاع بسنجیم بعد از ۱۰ بار تا کردن ضخامت کاغذ بدست آمده ۱۰۲۴ برابر حالت اولیه می شود و در مرحله ۱۱ ام۲۰۴۸ و در مرحله ۱۲ ام ۴۰۹۶

یعنی در مرحله دوازدهم باید ۴۰۹۶ برگ را تا کنیم که ضخامتی برابر با حدود ۵۰ سانتی متر که کار خیلی دشوار و تقریبا ناممکن است

 

 

کاربرد مثلث در موسیقی

مثلث از ابتدایی ترین اشکال هندسی بوده که انسانها در هنر از آن استفاده میکردند، بدون شک اولین نوع از انواع مثلث هم که در هنر از آن استفاده شده مثلث متساول الاضلاع بوده است. اهرام مصر نمونه بسیاری قدیمی (حدود 2800 سال پیش از میلاد) از کاربری مثلت در هنر معماری قدیم بوده است. نمونه های دیگر از استفاده از مثلث در هنر تمدن های قدیم را می تواند در کاشی کاری های دیواره معابد Pompeii در نپال نیز مشاهده کرد.

معروف هست تالس (640-550 سال پیش از میلاد) که پدر ریاضیات، نجوم و فلسفه یونان باستان بوده از شاگردان خود می خواهد که به مصر سفر کنند تا از پیشرفت علوم در آن تمدن اطلاعات لازم را کسب کنند و فیثاغورث (Pythagoras) از اولین افرادی بوده که این دستور را می پذیرد و به مصر سفر میکند. فیثاغورث از بنیانگذاران علمی موسیقی در جهان بوده و اغلب از هندسه برای مدل کردن استفاده می کرده، می خواهیم با استفاده از تجربیات او سلسه مطالبی را پیرامون ارتباط موسیقی با علوم هندسه، فیزیک و ریاضی آغاز کنیم. 
 

 موسیقی را می توانیم به روشهای مختلف مدل کنیم برای شروع کار ساده ترین روش را انتخاب میکنم که عبارت است از مدل کردن عمودی موسیقی یاهمان هارمونی. این روش مدل کردن به موسیقیدان ها کمک می کند تا هنگام فکر یا گوش کردن به هارمونی تصویر بهتری از نت های موسیقی داشته باشند بخصوص برای نوازندگان سازغیر از پیانو.

یک دایره در نظر بگیرید و آنرا به دوازده قسمت مساوی (یک اکتاو کروماتیک) تقسیم کنید و نت ها را به ترتیب روی هر قسمت بنویسد مانند شکل. یکی از ساده ترین اشکال هندسی که در این دایره تقسیم شده می توان ساخت مثلت متساوی الاضلاع می باشد. که اگر آنرا بسازید و به آن دقت کنید تفسیر موسیقی آن یک آکورد افزوده خواهد بود. حتما" شنید که آکوردهای افزوده جدای از اینکه معکوس باشند یا نه چهار حالت بیشتر نیستند که دایره فوق این موضوع را بسادگی نمایش میدهد چرا که اگر راس بالایی مثلث را در جهت عقربه های ساعت حرکت دهیم تا رسیدن به نت E و انطباق دوباره روی خود، می تواند سه حالت دیگر را به خود بگیرد. همچنین به وضوح در شکل می توان دید که یک آکورد افزوده از سه فاصله (که در اینجا هرکدام یک ضلع مثلث هستند) یکسان معادل 4 نیم پرده تشکیل شده است. 

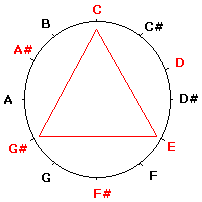
مثلث متساول الاضلاع معادل یک آکورد افزوده

شما باز هم می توانید مثلث های دیگری درست کنید. به شکل بعدی نگاه کنید که آکوردهای دو ماژور و لا مینور را نمایش میدهد. این دو مثلث (آکورد) خصوصیات جالبی دارند اولا" اضلاع آنها باهم برابر است، ثانیا" نسبت به خطی که از D کشیده میشود و به G# خطم میشود متقارن می باشند، حتما" می دانید که مینور نسبی گام دو ماژور، لامینور می باشد. به این طریق شما می توانید یک روش ساده برای پیدا کردن گامهای مینور و ماژور نسبی پیدا کنید، هر چند اینکار در پیانو بخاطر وضوح دیداری که چیدمان نت ها وجود دارد ساده می باشد.

مثلث های متساوی الساقین هم جالب هستند یکی از آنها آکورد sus2 را تشکیل میدهد که در شکل مشاهده میکنید و همچنین میتوانید آکوردهای کاسته را نیز باز با یک مثلث متساوی الساقین درست کنید. اگر دقت کنید این مثلث متساوی الساقین حالت آکورد sus2 برای C و حالت آکورد sus4 برای G دارد. بنابراین می توان به ارتباط نزدیک آکوردهای sus در حالت های 2 و 4 برای فاصله های پنجم با یکدیگر پی برد. این نکته هم جالب خواهد بود اگر شما راس D در این مثلث را نسبت به راس C قرینه کنید به آکورد sus2 دیگری می رسید که یک پرده عقب تر است آکورد Csus4 قرار دارد.

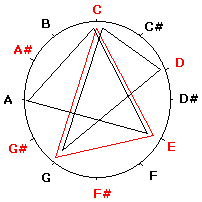
آکوردهای بزرگ، کوچک، sus2 و sus4

شما می توانید دامنه مدل کردن را ادامه دهید و راجع به سایر مثلث ها فکر کنید، همچنین می توانید آکوردهای چهار صدایی را با انواع چهار ضلعی ها مدل کنید. سئوالی که پیش می آید این است که آیا هستند افرادی که با شنیدن موسیقی این اشکال در ذهن آنها نقش ببندد؟