زیباییهای ریاضی - اعداد
درود به همه دوستان . امیدوارم همگی خوب و خوش و خرم باشید.
تصمیم دارم ازاین به بعد هر پنج شنبه – البته اگه فرصت کنم – وبلاگ رو به روز کنم .فقط نکته ای که هست قصد دارم از این به بعد یه تغییراتی در محتویات وبلاگ بدم ، اونم اینکه برای اینکه مطالب عامه پسند باشه و همه دوستان بتونن استفاده کنن ، از اون حالت ریاضی فرمولی بیرون بیام و بیشتر مطالبی رو بنویسم که جنبه زیبایی و کاربردی داره .اون چیزهایی که ما در زندگی روزمره زیاد باهاشون برخورد میکنیم و همه از ریاضیات الهام گرفته اند. خوشحال میشم دوستان یاری کنن . امیدوارم همگی موفق باشید.
مطلبی رو که برای این پست انتخاب کردم در مورد شگفتی های اعداد هستن . البته اگه به وبلاگ ها و سایتهای ریاضی یه سر بزنین از این مدل مطالب زیاد می بینین ولی فکر کنم این مدلی رو ندیده باشین ، لااقل من یکی که به خیلی از سایت ها و وبلاگ های ریاضی سر زدم ندیدم .
میگن افلاطون از تماشای رابطه

سیر نمیشد ، و ساعات زیادی حیرت زده این رابطه رو نگاه میکرد.حالا ، اگه روابط زیر رو دیده بود چه میکرد !

اگرچه این گونه روابط هماهنگیها و زیباییهای خاص خودشو دارن ، و ممکنه مایه ی شکفتی اشخاص عادی یا مبتدی در تئوری اعداد باشند ، اینگونه زیبائها نیست که ریاضیدانها رو به این علم میکشد ، بلکه به قول گاوس در یکی از نامه هاش به سوفی ژرمن ، بانوی ریاضیدان و دانشمند فرانسوی :
« کمال زیبایی آنیتهای دلفریب این علم شریف عالی فقط بر کسانی آشکار می شود که جرات فرو رفتن در اعماق آن را دارند.»
بعد از نامه آقای گاوس بریم سراغ شگفتی بعدی !
بعضی از شگفتی هایی که در کتابهای ریاضی میان توجیهاشون دشواره و به وسیله ی قسمتهای پیشرفته تئوری اعداد انجام میگیره . از جمله رابطه جالب زیر : (به اعداد و تکرار اعداد در ارقام بعد از اعشار توجه کنید)

حالا بیایم بحث رو کمی تخصصی تر کنیم و به یه نتیجه جالب برسیم و بعد از اون هم یه شگفتی ساده و سپس یه سورپرایز!
اتحاد زیر رو در نظر بگیرین

به ازاء  نتیجه می شود
نتیجه می شود

از اتحاد

روابطی از قبیل

و غیره حاصل می شود.
بالاخره ، از اتحاد

بازاء  نتیجه می شود
نتیجه می شود

و غیره .
عدد  خاصیت جالبی دارد. از رابطه ی
خاصیت جالبی دارد. از رابطه ی  نتیجه می شود ،
نتیجه می شود ،

پس ، به ازاء  ، عدد
، عدد  عددی است ۹ رقمی که همه ی ارقامش مساوی k است . اینک
عددی است ۹ رقمی که همه ی ارقامش مساوی k است . اینک
عدد20 رقمی  را اختیار می کنیم . از رابطه ی
را اختیار می کنیم . از رابطه ی

نتیجه می شود ،

مطلب بعدی که هم ساده و هم جالبه اینکه که ، چند نمونه ضربهایی که هریک از ارقام 1 تا 9 درست یک بار در آنها دیده می شود:

واما ضربهای زیر رو دقت کنید و بعد به ارقام و نمایش آنها !

یا

و

یا

حالا نظرتون در مورد این دو تا چیه !

یا

امیدوارم زیبائیهای ریاضی و شگفتی های آن براتون جالب بوده باشه . امیدوارم همیشه شاد و سربلند باشید. به امید دیدار
بدرود




 داریم
داریم 
 به طور یکتواخت در بازه
به طور یکتواخت در بازه  همگراست .
همگراست .


 با استفاده از استدلال استقرایی مساله را در نظر می گیریم .
با استفاده از استدلال استقرایی مساله را در نظر می گیریم .  مساله برقرار است.
مساله برقرار است. ثابت و
ثابت و  . در این حالت داریم :
. در این حالت داریم :

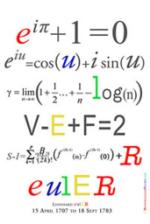 ریاضیات علم آموختن اندیشیدن است نه آموختن اندیشه ها!
ریاضیات علم آموختن اندیشیدن است نه آموختن اندیشه ها!